Chapter 10. Manifold spaces
I wish now to talk about space in geometrical terms to complement the more experiential account given in preceding chapters.
I have defined matrix space as the space of the real or Euclidean shape of physical things; the space out of which the perspectives of ordinary perception emerge. It is the space of the true cube or cylinder or any other solid, as distinct from perspectival space which distorts the true shape of things. And I have proposed that matrix space can be directly apprehended by psi awareness; and that this apprehenesion is restricted, in ordinary consciousness, to correcting the distortions of immediate physical perception – with respect to shape, size and relative position. With further training, you can extend your psi awareness of matrix space beyond the limits of what is being looked at with the eyes – as I proposed in section 13 of Chapter 7.
The geometry of Euclid seems to define accurately enough the spatial matrix of our immediate physical perception of the world, but it would be wrong to identify matrix space exclusively with Euclidean space.
1. Non-Euclidean geometry
It was centuries before human beings realised the distinction between mathematical space and actual space. In 300 BC, Euclid martialled the results of the Greek mathematicians of the classical period into his celebrated Elements. And for over 2000 years – until the discovery of non-Euclidean geometry by Bolyai, Gauss and Lobachevsky in the 1820s – it was assumed that to talk about the properties of space as such, was to talk in terms of Euclidean geometry. Geometry meant the geometry of physical space, and that geometry was Euclid’s. It was taken as self-evident that the consistency and elegance of Euclid’s system represented the final and absolute word about space.
The emergence of non-Euclidean geometry was an epoch-making event in the history of thought. A simple and liberating inspiration reached three men almost simultaneously, but quite separately. And it marked the turning point from an era of mental absolutism to an era of mental relativity. Euclid’s parallel postulate – that there can only be one line parallel to a given line through a point external to it – had always seemed less intuitively secure than his other postulates. Bolyai, Gauss and Lobachevsky decided to give it special status no longer.
They and their followers showed that by replacing it by one or other of its two contradictory forms – there can be no line parallel to a given line through a point external to it, and there can be many lines parallel to a given line through a point external to it – perfectly consistent geometries could be built up with many theorems that are quite inconsistent with the equivalent Euclidean theorems. And it was later found that both the Euclidean and the two non-Euclidean geometries were relative to a specialised treatment of certain aspects of the more general space of projective geometry.
The mathematical notions of certainty and absolute truth were shaken. The relativity of postulate systems was asserted: the truth of Euclidean geometry is not absolutely but only relatively true. The realisation of this by scientists, mathematicians and philosophers has had an immense influence on the mental climate of our age.
2. Projective geometry as the source of metric geometries
Euclidean and non-Euclidean geometries deal with metric properties. They state systematically the relations between sizes of angles, lengths of lines, areas, as these relations appear in different figures.
Projective geometry, founded by Desargues in 1639, is concerned solely with the non-metric properties of figures, when these figures undergo projection and section. Project the same circle from many different angles upon a screen, then projective geometry will ask what properties are common to all these different projections. The common properties will not be metric ones, for there will be no constancy of width, of area, of subtended angles, and so on.
Projective geometry emerged into a fully developed science during its revival in the nineteenth century. This was because mathematicians had greatly increased their ability to handle the notion of geometrical infinity. The infinite is taken actively into account in the shaping of projective space.
So think of an archetypal projective space, free of any specific metric properties, in which our only concern is with those properties of figures that are invariant under any number of projective transformations. We are not concerned with any exact measurement relations as such, but only with ratios and relative proportions. This is a mobile, metamorphic kind of space.
The deepest law of this projective space is the polarity of point and plane, the locus of no extension and the locus of infinite extension. And out of the universal forms of projective space, different geometric spaces with different metric properties can be developed and differentiated. It all depends on what element in non-metric, projective space we select and fix or freeze into a unique entity – a given absolute – which then determines a sub-space with certain definite metric properties.
Each metric geometry, in fact, is simply projective geometry with special relation to an absolute conic. Each arises from the different geometric character we ascribe to the absolute or infinite region.
If we take as our absolute in projective space an infinite plane bearing an imaginary circle, then this invariant form will determine the metric properties of Euclidean (parabolic) space. This, of course, is the space we identify with the space of everyday objects. And in this space there can only be one line parallel to a given line through a point external to it, the angles of a triangle always add up to 180 degrees, and so on.
If we make our invariant absolute an imaginary quadric, this governs and determines the metric properties of the non-Euclidean space known as Riemannian (elliptic) space. In this space there are no other lines parallel to a given line through a point external to it; and the angles of a triangle always add up to more than 180 degrees.
A concrete representation of this kind of space is provided by the surface of a sphere. On a sphere, a straight line – defined as the shortest distance between two points – becomes a ‘great circle’, which is the shortest distance between two points on a spherical surface. On a sphere there are no parallel lines of the Euclidean sort, for each great circle intersects every other at two points. And when any three great circles intersect to form a triangle, the sum of its angles is always greater than 180 degrees.
Finally, if we make invariant in projective space a real non-ruled quadric, this determines the metric properties of the non-Euclidean space known as Lobachevskian (hyperbolic) space. Here there is more than one line parallel to a given line through a point external to it; and the angles of a triangle always add up to less than 180 degrees. A concrete representation of this kind of geometric space is provided by the concave surface of a pseudosphere.
To everyday objects we ascribe the geometrical properties of Euclidean space, because this is the simplest of logically possible forms, and seems to make sense of our immediate perceptual experience. But the logical simplicity of Euclid fails to do justice to the inherent complexity of the physical universe at large.
So attempts to conceptualise the space which astronomical telescopes probe, as in the general theory of relativity, led to the view that a non-Euclidean geometrical space of the Riemannian type might have greater relevance. What type of geometrical representation – Euclidean, non-Euclidean or pseudo-Euclidean – is best suited to symbolise the wider view of the physical universe is still under discussion.
The significance of Einstein’s idea of applying a non-Euclidean geometry to the universe at large was that it made fully explicit the relativity of spatial concepts. It broke up the idea of one absolute, universal and homogeneous space exhibiting everywhere Euclidean properties. It suggested, rather, that the geometrical properties of space are relative to the standpoint of the observer, his assumptions, the range of his vision, and the purposes he has in mind. Different spaces can have different properties as a function of different intentions and beliefs. Or to put it another way, the properties of any space are inseparable from the structures of the consciousness that embraces it.
This account starts to echo the doctrine of powers view – that different spaces are different forms of the archetypal creative energy of universal consciousness.
3. Matrix within matrix
I said in the introduction to this chapter that it would be wrong to identify matrix space exclusively with Euclidean space. I can now say why. When my awareness embraces the matrix space of this room, say, by being simultaneously in all its eight corners, the structure of my awareness is informed by the logic of Euclidean metric geometry.
But, as we have seen in the previous section, this Euclidean matrix space is itself a limited and limiting ‘perspective’ of consciousness on a subtler, deeper and richer matrix space: the non-metric, mobile, metamorphic, projective space of ratios and relative proportions. And here the structure of my awareness is informed by the logical polarity of point and plane.
Let’s see now if we can relate this geometrical account of space to the experiential account of the expansion of consciousness given in earlier chapters, especially the section 13 of Chapter 7.
I can liberate my awareness spatially in two distinct steps. I can expand it from limited perspectives in physical space to a more extensive awareness in Euclidean space – of the ‘fixed’ subtle matrix of physical forms. And then I can expand it beyond that to the archetypal, projective matrix of the Euclidean matrix – to the subtler, mobile subtle matrix of the fixed subtle matrix of physical forms.
Indeed, clairvoyant exploration of the Euclidean matrix of, say, a room already seems to be done from the projective matrix, with many viewpoints from the lines of interacting planes. So we view the first step from the standpoint of the second.
However, we have to be cautious about this geometricising of experience. We must be careful not to identify experiential space with geometrical space. Geometrical knowledge develops and changes. It can inform and illuminate our experience of different kinds of space. Yet we may have spatial experiences that transcend the limits of geometrical advance. And we can have misfits: we may apply the wrong kind of geometry to certain kinds of spatial experience.
4. The fourth dimension
In the case of four dimensional space, imagination and analytic thought seem on their first encounter to be incompatible. It is easy to define a space of four dimensions in terms of coordinate or analytical geometry. It has four independent directions or dimensions at right angles to each other; and four coordinates will be needed to identify spatial entities in it. But it is difficult to imagine or visualise it.
The line, the surface and the volume are respectively spaces of one, two and three dimensions. We see at once that two points bound one line, four lines bound one square, six squares bound one cube. But if we continue this sequence and say that eight cubes bound one four-dimensional figure which will have a symmetrical eight-sided aspect to four independent directions – then the imagination gives out. Any attempt to visualise such a figure flounders in chaotic incoherence.
But there is another, more experiential, approach with which the imagination can do some business. We know that from our three-dimensional point of view we can look inside, grasp fully the total form of, a two-dimensional figure such as a circle or square. If our line of vision is at right angles to the central point of any such plane figure, then for all practical purposes we see it as it really is: we see its true Euclidean shape, inside and out, all at once. But a two-dimensional being could only get a limited, partial and distorted view of a bit of the inside, or a bit of the outside.
By analogy, we can imagine that an intelligence in four-dimensional space can look inside, grasp fully the total form of, any three-dimensional volume such as a cube or a sphere. Whereas our three-dimensional perspective of a cube is only a limited and distorted view of part of the outside of it, every part of its contents could be seen from a four-dimensional standpoint. The whole thing could be seen, inside and out, as it really is, all at once. But this is what is involved in entering matrix space, as described in section 13, Chapter 7; and in entering fully one’s own matrix body as described in section 2, Chapter 9: embracing a three-dimensional volume fully, inside and out, all parts being simultaneously entertained in awareness.
So we can say that four-dimensional space is a non-perspectival awareness, all at once, of the total spatial gesture of a three-dimensional figure. On this account, the fourth dimension of space is a certain holistic state of awareness. In the fourth dimension, space and consciousness are coterminous.
The fourth dimension – a direction at right angles to the three directions of physical space – is an inclusive and encompassing way of being aware of these three directions: it is a spatial form of consciousness. Now the account of four-dimensional space given by analytical geometry is such that an equation with four variables could represesent a three-dimensional stretch in a space of four dimensions. In other words, equations with four variables give an algebraic account of consciousness of matrix space. This launches us into the mathematics of altered states of consciousness. But I am not competent to proceed further.
5. Modes of spatial experience
There is one basic question I have not so far considered. What is the relation between this holistic four-dimensional grasp, all at once, of a three-dimensional shape and the multiple clairvoyant views of such a shape from peripheral lines on the clairvoyant plane of vision?
It is equivalent, at the physical level, to the difference between feeling one’s body shape from within by sensation from its tissues, and looking at its shape with one’s eyes. In my physical body I have these two complementary modes of spatial experience: feeling or sensing my place in space, and seeing where I am. And mediating between them is moving through space. I can be in space, see in space and move in space.
The same modes of spatial experience seem to apply at the subtle level, but each in a much more emancipated form. For subtle awareness, it seems that I can be in space, in the holistic four-dimensional all-at-once sense, not just here where my subtle body is, but there where some other entity is. And I can see in subtle space not just from one central viewpoint, but also from many peripheral viewpoints. And may subtle body movement in subtle space can at times seem as rapid as thought itself, and can negotiate different spaces that express different forms of consciousness and energy.
6. The fifth and sixth dimensions
Suppose you have a four dimensional grasp of a three dimensional figure. This means, according to section 4 just above, that your awareness grasps the true shape of the figure all at once, inside and out, as it really is. What does it mean if your awareness then expands into a further and fifth dimension of space? What is it to have a five dimensional grasp of a four dimensional figure? Or, to put it another way, what is it to know all-at-once your knowing all-at-once of a three dimensional figure?
One thing it could mean is that you shift into a space within four-dimensional space. The word ‘within’ here is used by analogy. I don’t mean ‘within’ in the sense of within the house or within the box – that is ordinary three-dimensional talk. It is more akin to what I mean when I say that the gaze is within the eyes, a person is within his body, or life is within the leaf. But is also a bit more rigorous than these examples indicate.
When I go out of my body into the other world (not just having an ectosomatic view of this world) I am in a quite distinct domain which is not located ‘in’ physical space, in the ordinary sense of this word ‘in’. It is not in it like an orange is in it, or the moon is in it. But the other world domain I visit clearly does have some kind of spatial relationship to this world: for going out of the body to that domain is itself a spatial transition.
It is, I suppose, logically possible for there to be two distinct spaces that are not themselves spatially related. Indeed, one contemporary theologian, John Hick, has conceived the after-life in this way: as a kind of instantaneous resurrection at the moment of death in a space of which it makes no sense to ask where it is in relation to the space of this life. But my experience is different, not I hasten to add of dying, but of going from this world to the other: as I say, this ‘going’ is a spatial business.
It seems to me that the other world is within, in the sense of interpenetrating, this world: an interpenetration that somehow supports this world and provides the framework or matrix for it; and also an interpenetration that in other respects is quite independent, functionally, of this world – in the sense that many things can go on in the other world without having any obvious effect on what is going on in this world.
Interpenetration also means that you can in some sense say where some independent other-world domain is in relation to the space of this universe. This ‘where’ may be fixed or mobile. So I may say there is a domain of subtle space within the physical area between the earth and its moon: this would be a fixed kind of co-location of the two worlds. Or I may say that there are domains of inner space that ‘move through’ the physical area, say, of the solar system: here the co-location shifts around.
As well as other-world domains interpenetrating the space of this universe, they also, of course, have more inclusive logical or geometrical parameters than physical space. And the energy frequencies of events within them are also different: usually, it seems, much higher.
By extending this notion of the interpenetration of spaces, we may say that we enter a six dimensional space when we are conscious in and of a first other-world domain that interpenetrates a distinct and second other-world domain, which in turn interpenetrates the all-at-once four dimensional matrix of the physical realm. Each more comprehensive space is a matrix of the space it transcends. And just as in the four dimensional matrix of physical space you can know any three dimensional volume both within and without all at once; so also in the fifth dimensional matrix you can know any four dimensional space simultaneously from the ‘inside’ and the ‘outside’; and so on in the sixth. Figure 10.1 gives simple portrayal of the hierarchy of spaces, grounded in mahabindu, the Great Point.
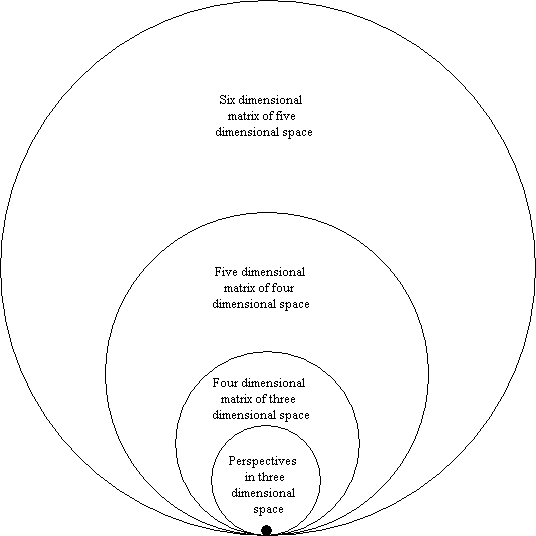
Figure 10.1 The hierarchy of spaces
This hierarchy of spaces is, on the doctrine of powers view, also a hierarchy of the structures and energies of universal consciousness. Each higher dimension comprehends all the other dimensions within it, is more intense in its degree of consciousness, and manifests higher frequencies of energies.
So we get a conjectural model of a universe of manifold spaces: there is the first subtle realm which transcends yet interpenetrates the second subtle realm, which in turn transcends yet interpenetrates the four-dimensional subtle matrix of the physical world. And all this structured diversification is of consciousness itself, of which my consciousness and your consciousness are illusorily restricted parts. We can break out of the illusion, and get going on the wider reaches of spatial reality.
Roughly speaking, the first and second subtle realms mentioned here correspond to the higher subtle level, and the interaction between the second subtle realm and the subtle matrix to thelower subtle level, of Grof’s cartography of transpersonal states (Grof, 1988: 39).
7. Dimensional clusters
We grasp the first three dimensions of space in one go. We don’t first learn to master one dimension, the line, then two dimensions, the plane, then three dimensions, the solid and the enclosed or open space. We take them on board in a cluster. They come in our ordinary consciousness together.
I believe it is essentially the same with the second three dimensions of space, the fourth, fifth and sixth. When I enter my levity line and thence into all-at-once four dimensional awareness of the subtle matrix of my physical body, at the same time I have five dimensional awareness of the way in which my subtle body proper interpenetrates my subtle matrix and thence my physical body. Also at the same time I have at least incipient six dimensional awareness of subtle domains within and beyond my subtle body frequencies: because I can choose to open myself up to these higher frequencies and make my six dimensional awareness explicit.
There is nothing particularly mysterious, problematic or esoteric about this experiential cluster of the fourth, fifth and sixth spatial dimensions. It’s just a matter of doing the exercises that open up your awareness at the matrix level, and noticing how the cluster comes. At any rate, it is not really any more mysterious than how the first three dimensions of line, plane and solid all come together.
The first cluster initiates us into spatial extension – the without of space. The second cluster initiates us into spatial intension – the within of space. I give the word ‘intension’ here a new technical meaning. In relation to any domain of subtle space, it refers to three things: the degree or intensity of consciousness of which that space is the form; the degree or frequency of its energies; and the degree to which it includes, by virtue of its multi-dimensional structure, other spaces which it interpenetrates and yet transcends.
Physical birth launches us into the first cluster, physical death into the second cluster – when our consciousness starts to function explicitly in the subtle body. But we need not wait to be born into the subtle body at death. We can start to become our own ally now, awakening ourselves to explicit subtle action in the midst of earthly life.
Experience of the subtle realms: